 =
= 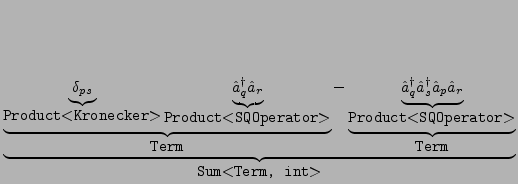
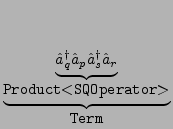
Now we have designed and implemented all objects we identified in our original problem. However, we already mentioned that it will be useful to define an additional object Term. The convenience of an object Term is related to the mathematical concept of closedness (in the sense of group theory): The application of the anticommutation rule will transform a pure product of second quantized operators into a sum of a pure product of second quantized operators and a product of second quantized operators multiplied by product of Kronecker symbols. All objects to represent this algebraic structure have already been designed except for the mixed product of second quantized operators and Kronecker symbols. Exactly this shall be a Term. We shall illustrate this using the following example:
 =
= 
Now you see the expressive power of templates once more.
Here is the source: Interface: Term.H
1 #ifndef Term_H
2 #define Term_H
3
4 #include "Product.H"
5 #include "SQOperator.H"
6 #include "Kronecker.H"
7 #include "Sum.H"
8
9
10 #include <iostream>
11
12 using namespace std;
13
14 /*!
15 A term consists of a Product of SQOperators and a Product of Kroneckers
16 */
17 class Term {
18 public:
19 //! construct from Product<SQOperator>, Product<Kronecker> will be empty
20 Term(Product<SQOperator> const & opProd);
21
22 //! construct from Product<SQOperator> and Product<Kronecker>
23 Term(Product<SQOperator> const & opProd, Product<Kronecker> const & kProd);
24
25 //! return contained Product<SQOperator>
26 Product<SQOperator> opProd() const;
27
28 //! return contained Product<Kronecker>
29 Product<Kronecker> kProd() const;
30
31 //! artificial ordering
32 bool operator < (Term const & t) const;
33
34 //! calculate normal ordering
35 Sum<Term, int> normalOrder() const;
36
37 //! calculate normal ordering, fully contracted terms only
38 Sum<Term, int> normalOrder_fullyContractedOnly() const;
39
40 private:
41 Sum<Term, int> normalOrder(bool fullyContractedOnly) const;
42
43 Product<SQOperator> _opProd;
44 Product<Kronecker> _kProd;
45 };
46
47 //! output operator for Term
48 ostream & operator << (ostream & o, Term const & t);
49
50 #endif
Implementation: Term.C
1 #include "Term.H"
2
3
4 Term::Term(Product<SQOperator> const & opProd) :
5 _opProd(opProd) {}
6
7 Term::Term(Product<SQOperator> const & opProd, Product<Kronecker> const & kProd) :
8 _opProd(opProd), _kProd(kProd) {}
9
10
11 Product<SQOperator> Term::opProd() const
12 { return _opProd; }
13
14 Product<Kronecker> Term::kProd() const
15 { return _kProd; }
16
17
18 bool Term::operator < (Term const & t) const
19 {
20 if ( _kProd<t._kProd )
21 return true;
22 if ( t._kProd<_kProd )
23 return false;
24 return _opProd<t._opProd;
25 return true;
26 }
27
28
29 ostream & operator << (ostream & o, Term const & t)
30 {
31 o << t.kProd();
32 if ( t.kProd().size()>0 && t.opProd().size()>0 )
33 o << "*";
34 o << t.opProd();
35 return o;
36 }
Let's test it: Term_Test.C
1 #include "Term.H"
2 #include "Sum.H"
3
4 using namespace std;
5
6 int main()
7 {
8 Product<SQOperator> p;
9
10 p *= SQOperator('i');
11 p *= SQOperator('j');
12 p *= SQOperator('A');
13 p *= SQOperator('B');
14
15
16 Product<Kronecker> k;
17
18 k *= Kronecker('x', 'y');
19 k *= Kronecker('p', 'q');
20
21 Term term(p, k);
22
23 cout << term << endl;
24
25 Sum<Term, int> s;
26
27 s += term;
28 s += term;
29 s += term;
30
31 cout << s << endl;
32
33 return 0;
34 }
The output is (download
tarball
into a fresh directory, extract, compile and link with g++ *.C, run a.out)
d(xy)*d(pq)*i*j*A*B 3*d(xy)*d(pq)*i*j*A*B
This is no longer completely trivial...