
Next: Coupled Cluster Methods (CC)
Up: Perturbation Theory (PT)
Previous: Multi-reference perturbation theory
Toggle Background
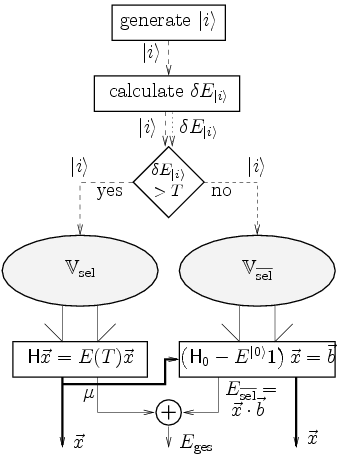
Out of a freely chosen reference space (not necessarily a CAS space) all
single and double exciatations are performed.
The method developed [9]
and later extended [10]
still uses the Epstein-Nesbet scheme for
selection purposes but the energy contributions from the non selected
configurations are no longer summed up. Instead the MR-MP2 equations are solved
within the expansion space of the non selected configurations.
The MP2 energy is simply added without any weighting factor
to the variational selected MRCI energy.
The following figure ![[*]](crossref.png) illustrates this scheme.
illustrates this scheme.
To solve (11) in a direct manner
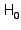 is evaluated in each iteration.
is evaluated in each iteration.
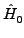 was chosen to be an effective one particle operator with the highest
contributing excitations beeing single ones. For implementation purposes
the internal/external separation
[11,12] is a powerful tool to neglect higher excitations
efficiently. Therefore the current implementation is based on the
internal/external separation and uses the same algorithms as the DIESEL-CI
[1].
The solution vector
was chosen to be an effective one particle operator with the highest
contributing excitations beeing single ones. For implementation purposes
the internal/external separation
[11,12] is a powerful tool to neglect higher excitations
efficiently. Therefore the current implementation is based on the
internal/external separation and uses the same algorithms as the DIESEL-CI
[1].
The solution vector 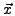 consists of the complete generated space
and may therefore not necessarily fit into the main memory.
This has to be taken into account for
the choice of the numerical method used to solve the linear equation system.
Typically a compromise between disk space consumption and iteration
cycles to gain convergence must be made.
It may be noted that this approach is a generalization of the CASPT2 method
[13] in its N-variant [14] form because it uses the same
consists of the complete generated space
and may therefore not necessarily fit into the main memory.
This has to be taken into account for
the choice of the numerical method used to solve the linear equation system.
Typically a compromise between disk space consumption and iteration
cycles to gain convergence must be made.
It may be noted that this approach is a generalization of the CASPT2 method
[13] in its N-variant [14] form because it uses the same
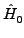 operator but has no comparably restrictive requirements on the reference
wave function. In the special case CASSCF orbitals are beeing used and the
reference set is chosen to be the CAS space one gets the same results if no
selection is done. However as this approach does not exploit the special
properties of the CASSCF reference function it is less efficient in the final
solution of the linear equation system because due to the missing partial
diagonalization of the Fock matrix the
operator but has no comparably restrictive requirements on the reference
wave function. In the special case CASSCF orbitals are beeing used and the
reference set is chosen to be the CAS space one gets the same results if no
selection is done. However as this approach does not exploit the special
properties of the CASSCF reference function it is less efficient in the final
solution of the linear equation system because due to the missing partial
diagonalization of the Fock matrix the
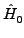 -matrix is less diagonal dominant.
-matrix is less diagonal dominant.


Next: Coupled Cluster Methods (CC)
Up: Perturbation Theory (PT)
Previous: Multi-reference perturbation theory
Michael Hanrath
2008-08-13
![[*]](crossref.png) illustrates this scheme.
illustrates this scheme.