

Next: Research interest / own
Up: Introduction
Previous: Introduction
Toggle Background
The coupled cluster wave function is given by
with
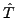 =
= 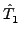 +
+ 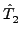 +... and
+... and
the cluster operator.
Inserting (13) into the Schrödinger equation we obtain
Multiplying by
e-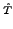 yields
yields
Projecting (15) onto
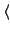
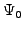 | and substituted determinants we get
non-linear equations for the energy E and the amplitudes tia,
tijab, ... respectively.
| and substituted determinants we get
non-linear equations for the energy E and the amplitudes tia,
tijab, ... respectively.
Michael Hanrath
2008-08-13