Introduction

Toggle Background

The CI methods use a linear ansatz for the wave function according to

$$\Psi_{{\rm CI}}^{} \rangle \sum_{{\vert i\> \in {\mathbb M}}}^{} \rangle$$ (1)

The CI eigenvalue problem is often derived from the variation principle. We shall choose here a different derivation: Inserting ((1)) into the Schrödinger equation

$$\hat{H} \Psi \rangle \Psi \rangle$$ (2)

results in

$$\hat{H} \Psi_{{\rm CI}}^{} \rangle \tilde{E} \Psi_{{\rm CI}}^{} \rangle \tilde{\Psi} \rangle$$ (3)

introducing |$\tilde{\Psi}$$\rangle$ since |$\Psi_{{\rm CI}}^{}$$\rangle$ is an approximation of |$\Psi$$\rangle$ and is not exact. Projecting (3) onto $\langle$j| and assuming $\langle$j| i$\rangle$ = $\delta_{{ji}}^{}$ yields

$$\sum_{{\vert i\> \in {\mathbb M}}}^{} \langle \hat{H} \rangle \langle \tilde{\Psi} \rangle$$ = (4)

$$\sum_{{\vert i\> \in {\mathbb M}}}^{} \Psi_{j}^{}$$ = (5)

Now the idea is to eliminate the projection of the error |$\tilde{\Psi}$$\rangle$ onto the basis $\mathbb {M}$ corresponding to $\Psi_{j}^{}$ = 0. Consequently, (5) reads as a usual eigenvalue. Summarizing, we have transformed the problem of finding an eigenfunction into a problem of finding an eigenvector. The whole derivation is simple and straightforward. A great advantage of the linear CI ansatz is that there is no "special" basis function making the generalization of CI to the multi-reference case trivial.

Full CI
Solving the CI problem in the full antisymmetric many-body space spanned by the one-particle basis is called full CI. Although the computational cost for a full CI calculation scales exponentially with the size of the system the obtained solution is still not exact due to the limitation of the one-particle space. However, full CI calculations are very important for benchmark calculations of other methods since they provide the best possible solution within a given one-particle basis.

Truncated CI
The the full CI expansion is rather inefficient because most of the expansion coefficients are very close to or virtually zero. Starting from an SCF calculation usually single and double spin orbital substitutions in a Slater determinant yield a reasonable approximation (CISD). One may systematically complete the space by including triples T, quadruples Q and higher substitution levels in the original Slater determinant (CISDT, CISDTQ, ...) and reach the full CI limit. Writing the CI-wavefunction in terms of excitation operators we get

$$\Psi_{{CI}}^{} \rangle \rangle \sum_{{\hat \tau_i \in \mathbb T}}^{} \hat{\tau}_{i}^{} \rangle$$ =

$$\mathbb {T} \bigcup_{{i_1\ldots i_m \in {\mathbb O} \atop a_i\ldots a_m\in {\mathbb V}}}^{} \hat{a}^{\dagger}_{{a_1}} \hat{a}^{\dagger}_{{a_m}} \hat{a}_{{i_m}}^{} \hat{a}_{{i_1}}^{}$$ =

$\mathbb {O}$: occupied space, $\mathbb {V}$: virtual space and we may draw an excitation graph as follows:

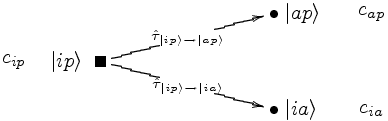
Multi-reference CI (MRCI)
There may be situations (e.g. spatial or spin degeneracy, dissociation, excited states, transition states) when the simple effective one-particle picture of the Hartree-Fock approach using a single determinant is no longer a valid approximation. As a consequence there is more than one dominant determinant in the CI expansion. For a reasonable approximation one should still include at least single and double substitution from each reference. This leads to the concept of multi-reference CI. The expansion set is given by the unified set of all n-fold substitutions from each reference and we may write the MRCI wave function as:

$$\Psi_{{MRCI}}^{} \rangle \sum_{{\mu}}^{} \mu \mu \rangle \sum_{{\mu}}^{} \sum_{{\hat \tau_i(\mu) \in \mathbb T(\mu)}}^{} \red \mu \hat{\tau}_{i}^{} \mu \mu \rangle$$ =

$$\mathbb {T} \mu \bigcup_{{i_1\ldots i_m \in {\mathbb O(\mu)} \atop a_i\ldots a_m\in {\mathbb V(\mu)}}}^{} \hat{a}^{\dagger}_{{a_1}} \hat{a}^{\dagger}_{{a_m}} \hat{a}_{{i_m}}^{} \hat{a}_{{i_1}}^{}$$ =

$\mathbb {O}$($\mu$): occupied space of |$\mu$$\rangle$, $\mathbb {V}$($\mu$): virtual space of |$\mu$$\rangle$ The excitation graph now looks as follows:

MRCI is very flexible and applicable to any type of problem. However, convergence to the exact result is rather slow. MRCI is neither size extensive nor consistent making it unfavorable for systems with a large number of electrons. It is mostly used for small systems with difficult wave function structures and for spectroscopic properties.

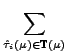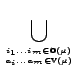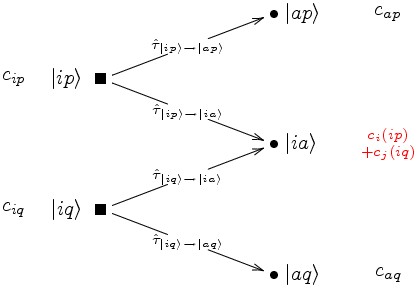
Individually selecting Multi-reference CI (MRCI)
In many applications the size of the wavefunction although truncated at single and double substitutions is still not manageable. But many (typically over 90%) coefficients of determinants are still almost zero. So it seems to be natural to select only those determinants which result in a significant contribution to the energy. In order to make sense this selection must of course be very cheap.