

Next: Research interest / own
Up: Perturbation Theory (PT)
Previous: Perturbation Theory (PT)
Toggle Background
In contrast to the Epstein-Nesbet scheme traditionally used
in individually selecting MRCI calculations
the Møller-Plesset partitioning [4] of the
Hamiltonian usually performs much better with respect to accuracy.
However,
the generalization of the Møller-Plesset theory to the multi
reference case needs more attention.
There are three implications from the generalization to the multi reference
case
[5,6,7,8]:
1. The mean field
approximation of the Fock operator within the SCF procedure has to be
generalized with respect to the multi reference state.
Accordingly the generalized Fock operator depends on the reference state
and has the following matrix elements:
fpq| 0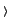 = hpq + = hpq + 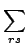 Drs| 0 Drs| 0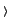 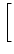 (pq| rs) - (pq| rs) -  (pr| qs) (pr| qs)![$\displaystyle \left.\vphantom{(pq\vert rs) - {1\over 2} (pr\vert qs)}\right]$](img64.png) |
(6) |
with hpq the representation of the core hamiltonian,
Drs| 0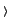 the one-electron density matrix
of the reference state | 0
the one-electron density matrix
of the reference state | 0 , (pq| rs) the two-electron integrals.
2. The Raighley-Schrödinger perturbation theory needs the reference
state to be an eigenfunction of the
, (pq| rs) the two-electron integrals.
2. The Raighley-Schrödinger perturbation theory needs the reference
state to be an eigenfunction of the
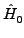 operator.
The introduction of the projection operators
operator.
The introduction of the projection operators
and the definition of
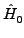 as
as
with E| 0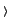 the reference energy
solves this problem from the other side as it defines the
the reference energy
solves this problem from the other side as it defines the
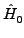 operator in a way that | 0
operator in a way that | 0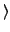 is an eigenfunction to
is an eigenfunction to
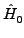 .
3. Due to the equations (7) and (9)
the excited slater determinants in the expansion space are no longer
eigenfunctions of
.
3. Due to the equations (7) and (9)
the excited slater determinants in the expansion space are no longer
eigenfunctions of
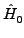 . As a consequence the
. As a consequence the
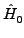 -matrix
is no longer diagonal and the very easily performed division by the orbital
energy differences within the evaluation of the single reference MP2 is
transformed into a solution of a linear equation system:
-matrix
is no longer diagonal and the very easily performed division by the orbital
energy differences within the evaluation of the single reference MP2 is
transformed into a solution of a linear equation system:
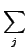 xj xj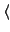 k| k|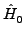 - E| 0 - E| 0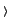 | j | j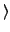 = - = - 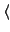 k| k|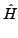 | |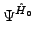 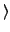 |
(9) |
or in short notation
Due to the size of
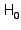 (11) can be solved by means of
an iterative procedure only.
The MP2 energy is then simply given by
(11) can be solved by means of
an iterative procedure only.
The MP2 energy is then simply given by
EMP2 = 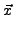 . . 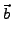 . . |
(11) |


Next: Research interest / own
Up: Perturbation Theory (PT)
Previous: Perturbation Theory (PT)
Michael Hanrath
2008-08-13