next up previous
Next: Cluster Operator Parameterization Up: Research interest / own Previous: Research interest / own

MRexpT Ansatz

Toggle Background


My contribution [15,16] to this development starts from the state-universal multi-reference coupled cluster (SU-MRCC) of Jeziorski and Monkhorst [17]. It is based on the ansatz

|$\displaystyle \Psi_{\lambda}^{}$$\displaystyle \rangle$ = $\displaystyle \sum_{\mu}^{}$c$\scriptstyle \lambda$$\scriptstyle \mu$e$\scriptstyle \hat{T}$($\scriptstyle \mu$)|$\displaystyle \mu$$\displaystyle \rangle$,    $\displaystyle \forall_{\lambda}^{}$ (15)

and contains a reference specific cluster operator

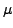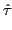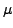$\displaystyle \hat{T}$($\displaystyle \mu$) = $\displaystyle \sum_{{\hat \tau(\mu) \in \mathbb T(\mu)}}^{}$t$\scriptstyle \hat{\tau}$($\scriptstyle \mu$)($\displaystyle \mu$)$\displaystyle \hat{\tau}$($\displaystyle \mu$) (16)

with

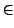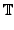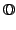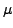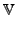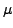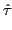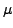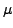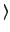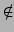$\displaystyle \mathbb {T}$($\displaystyle \mu$) = {$\displaystyle \hat{\tau}$($\displaystyle \mu$) $\displaystyle \in$ $\displaystyle \mathbb {T}$($\displaystyle \mathbb {O}$($\displaystyle \mu$),$\displaystyle \mathbb {V}$($\displaystyle \mu$))  |  $\displaystyle \hat{\tau}$($\displaystyle \mu$)|$\displaystyle \mu$$\displaystyle \rangle$ $\displaystyle \notin$$\displaystyle \mathbb {P}$} (17)

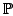
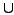
prohibiting excitations within the reference space. Substituting (16) into the Schrödinger equation the latter becomes underdetermined with respect to projection onto elements of 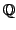$ \mathbb {P}$ $ \cup$ $ \mathbb {Q}$. The state universal ansatz overcomes this problem by employing the Bloch equation and considering as many states simultaneously as there are references.
Michael Hanrath 2008-08-13